Nonparametric estimation of time-varying reproduction numbers

Daniel J. McDonald

Mathematical modelling of disease / epidemics is very old

Daniel Bernoulli (1760) - studies inoculation against smallpox
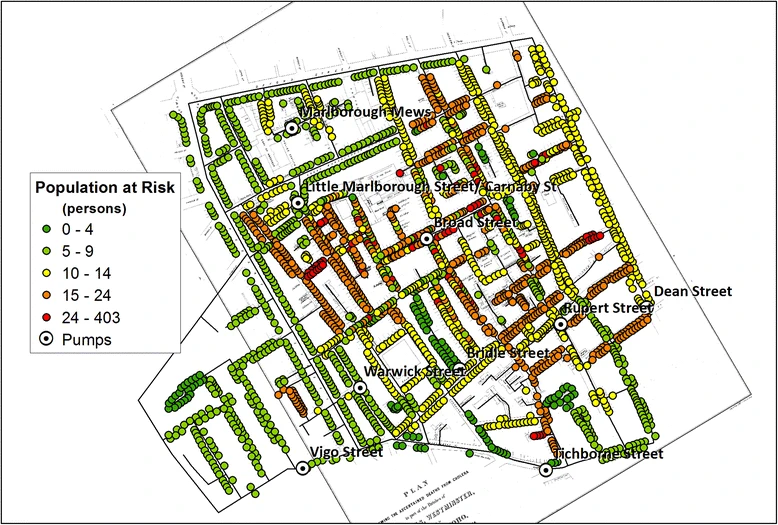
John Snow (1855) - cholera epidemic in London tied to a water pump
Ronald Ross (1902) - Nobel Prize in Medicine for work on malaria
Kermack and McKendrick (1927-1933) - basic epidemic (mathematical) model

Source: Shiode, et al., “The mortality rates and the space-time patterns of John Snow’s cholera epidemic map,” (2015)

\(R_0\) basic reproduction number

Dates at least to Alfred Lotka (1920s) and others (Feller, Blackwell, etc.)

The expected number of secondary infections due to a primary infection

\(R_0 < 1\) ⟹ the epidemic will die out

\(R_0 > 1\) ⟹ the epidemic will grow until everyone is infected

Source: Katelyn Jetelina, “YLE Newsletter,” 17 March 2025.

\(R_0\) is entirely retrospective

It’s a property of the pathogen in a fully susceptible (infinite) population
Each outbreak is like a new sample
To estimate something like this from data, the “bonehead” way is to
1. Wait until the epidemic is over (no more infections circulating)
2. Contact trace the primary infection responsible for each secondary infection
3. Take a sample average of the number caused by each primary
4. Possibly repeat over many outbreaks

Source: Guerra, et al., “The basic reproduction number (R0) of measles,” (2019).

Of course no one actually does that

Lots of work on how to estimate \(R_0\)

Effective reproduction number

Suppose \(s\)% of the population is susceptible

Then, “the” effective reproduction number \(R=sR_0\)

Allows you to reason about things like

The level of vaccine coverage necessary to prevent an outbreak from growing uncontrollably.

So, for measles, if \(R_0\approx 15\), the disease will die out if immunity is

\[ sR_0 \leq 1 \Longrightarrow 1-s \leq 1-1/R_0 \approx 93\% \]

\(R(t)\) — instantaneous reproduction number

The effective reproduction number in the middle of an outbreak
Some of the population is immune, others are infected, others susceptible

The expected number of secondary infections at time \(t\) caused by an earlier primary infection

\(f(a) \geq 0,\ \forall a\) — the rate at which an infection of age \(a\) produces new infections

\[ \begin{aligned} R_0 &= \int_{0}^\infty f(a)\mathsf{d}a, \\ g(a) &= \frac{f(a)} {\int_{0}^\infty f(a)\mathsf{d}a} = f(a) / R_0. \end{aligned} \]

Can allow \(g(t, a)\), hold this fixed for now.

The generation interval distribution \(g(a)\)

Source: US CDC Center for Forecasting Analytics, “Behind the Model.”

\(R(t)\) and \(R_t\) — renewal equation

\(R(t)\) is defined implicitly through the renewal equation

\[ x(t) = R(t)\int_0^\infty x(t-a)g(a)\mathsf{d}a, \]

where \(x(t)\) are infections at time \(t\).

In discrete time,

\[ x_t = R_t\sum_{a=0}^\infty x_{t-a}\widetilde{g}_a = R_t (x * \widetilde{g}). \]

And stochasticly,

\[ \mathbb{E}\big[x_t\ |\ x_1,\ldots,x_{t-1}\big] = R_t\sum_{a=0}^\infty x_{t-a}\widetilde{g}_a = R_t (x * \widetilde{g}). \]

Most estimators start here: \[ \mathbb{E}\big[x_t\ |\ x_1,\ldots,x_{t-1}\big] = R_t\sum_{a=0}^\infty x_{t-a}\widetilde{g}_a. \]

Assume \(\widetilde{g}\) is known
Model \(x_t\ |\ x_1,\ldots,x_{t-1}\) as Poisson or Negative Binomial
Turn some inferential crank

\(R_t\) for COVID-19 in the US

Source: US CDC Center for Forecasting Analytics

Estimating \(R_t\)

Data issues

\(x_t\) is Infections, but we don’t ever see those

Replace infections with cases
Replace generation interval with serial interval
Assume we have the serial interval

Serial interval distribution

Standard model for \(R_t\)

\[ \begin{aligned} \eta_t &= \sum_{a=0}^\infty y_{t-a}p_a,\\ \\ y_t\ |\ y_1,\ldots,y_{t-1} &\sim \textrm{Poisson}(R_t\eta_t). \end{aligned} \]

Using \(y\) instead of \(x\) to be cases or hospitalizations or deaths, incidence
Using \(p\) for serial interval distribution (discretized)
The MLE for \(R_t\) is just \(y_t / \eta_t\).
This has really high variance, but unbiased.
So everybody smooths it.

The state of the art

{EpiEstim} (Cori, et al., 2013)

Gamma prior on \(R_t\), but use a trailing window
Super fast computationally
Smoothness is ad hoc

{EpiFilter} (Parag, 2020)

State space model
One step smoothness: \(R_{s+1} \sim \textrm{Gaussian}(R_s,\ \alpha R_s)\)
Uses a discretized particle filter-type algorithm

{EpiLPS} (Gressani, et al., 2022)

Negative Binomial likelihood
Smoothness via \(\log(R_t\eta_t) = \mathbf{B}_{t,:}\beta\)
\(\mathbf{B}\) is cubic B-spline basis, weighted Ridge penalty on \(\beta\)
More priors, use Metropolis Adjusted Langevin Algorithm

{EpiNow2} (CDC + CFA, Abbott, et al., 2023ish)

Negative Binomial likelihood
Smoothness via a GP prior
Accommodates the sequence of delays from infection \(\longrightarrow\) ??
Adjusts for real-time issues like partial reporting
Big Bayesian MCMC in Stan. Very slow.

Our model

Let \(\theta_t := \log(R_t)\).

Use Poisson likelihood.

\[ \begin{aligned} \widehat{R} &= \exp(\widehat{\theta}) &\widehat{\theta} &= \mathop{\mathrm{argmin}}_\theta\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(k+1)}\theta\Vert_1 \end{aligned} \]

Convex, has a global optimum
\(\lambda\) controls smoothness relative to data fidelity
\(\ell_1\) penalty produces adaptive piecewise polynomials of order \(k+1\)
Near minimax optimal for functions with bounded total variation

Local adaptivity — \(\ell_1\) vs. \(\ell_2\)

Polynomial order, \(k=0\)

\[ \begin{aligned} D^{(1)} &= \begin{bmatrix} 1 & -1 & & & & \\ & 1 & -1 & & & \\ & & & \ddots && \\ & & & & 1 & -1 \end{bmatrix} \\ \\ &\in \mathbb{R}^{(n-1)\times n} \end{aligned} \]

Polynomial order, \(k=1\)

\[ \begin{aligned} D^{(2)} &= \begin{bmatrix} 1 & -2 & 1 & & & \\ & 1 & -2 & 1 & & \\ & & & \ddots && \\ & & & 1 & -2 & 1 \end{bmatrix} \\ \\ &= D^{(1)}D^{(1)}\\ \\ &\in \mathbb{R}^{(n-k-1)\times n} \end{aligned} \]

Polynomial order, \(k=2\)

\[ \begin{aligned} D^{(3)} &= \begin{bmatrix} -1 & 3 & -3 & 1 & & \\ & -1 & 3 & -3 &1 & \\ & & & \ddots && \\ & & -1 & 3 & -3 & 1 \end{bmatrix} \\ \\ &= D^{(1)}D^{(2)}\\ \\ &\in \mathbb{R}^{(n-k-1)\times n} \end{aligned} \]

Estimation algorithm

\[ \mathop{\mathrm{minimize}}_\theta\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(k+1)}\theta\Vert_1 \]

Estimation algorithm

\[ \mathop{\mathrm{minimize}}_{\theta,\ {\color{BurntOrange} \alpha}}\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(1)}{\color{BurntOrange} \alpha}\Vert_1\quad {\color{BurntOrange} \textrm{subject to}\quad \alpha = D^{(k)}\theta} \]

Estimation algorithm

\[ \mathop{\mathrm{minimize}}_{\theta,\ \alpha}\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(1)} \alpha\Vert_1\quad \textrm{subject to}\quad \alpha = D^{(k)}\theta \]

Alternating direction method of multipliers (ADMM)

\[ \begin{aligned} \theta &\longleftarrow \mathop{\mathrm{argmin}}_\theta\ \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \frac{\rho}{2}\Vert D^{(k)}\theta - \alpha + u \Vert_2^2 \\ \alpha &\longleftarrow \mathop{\mathrm{argmin}}_\alpha\ \lambda\Vert D^{(1)} \alpha \Vert_1 + \frac{\rho}{2}\Vert D^{(k)}\theta - \alpha + u \Vert_2^2 \\ u &\longleftarrow u + D^{(k)}\theta - \alpha \end{aligned} \]

Estimation algorithm

Alternating direction method of multipliers (ADMM)

\[ \begin{aligned} \theta &\longleftarrow {\color{Cerulean}\textrm{Proximal Newton / Fisher Scoring}} \\ \alpha &\longleftarrow {\color{BurntOrange}\textrm{Fused Lasso Signal Approximator}} \\ u &\longleftarrow u + D^{(k)}\theta - \alpha \end{aligned} \]

Solve sequentially for \(\Vert (D^{\dagger})^{\mathsf{T}}(\eta - y)\Vert_\infty = \lambda_1 > \cdots > \lambda_M=\epsilon \lambda_1\).