sim_SIR <- function(TT, N = 1000, beta = .1, gamma = .01) {
S <- double(TT)
I <- double(TT)
R <- double(TT)
S[1] <- N - 1
I[1] <- 1
for (tt in 2:TT) {
contagions <- rbinom(1, size = S[tt - 1], prob = beta * I[tt - 1] / N)
removals <- rbinom(1, size = I[tt - 1], prob = gamma)
S[tt] <- S[tt - 1] - contagions
I[tt] <- I[tt - 1] + contagions - removals
R[tt] <- R[tt - 1] + removals
}
tibble(S = S, I = I, R = R, time = seq(TT))
}CANSSI Prairies — Epi Forecasting Workshop 2025
Compartmental Models, Renewal Equations, and \(R_t\) Estimation
Lecture 3
Daniel J. McDonald
Outline
- Compartmental Models
- Operationalizing Compartmental Models
- What is \(R_t\)?
- Estimating \(R_t\)
- Results and features of
{rtestim}
1 Compartmental models
Mathematical modelling of disease / epidemics is very old
Daniel Bernoulli (1760) - studies inoculation against smallpox
John Snow (1855) - cholera epidemic in London tied to a water pump
Ronald Ross (1902) - Nobel Prize in Medicine for work on malaria
Kermack and McKendrick (1927-1933) - basic epidemic (mathematical) model
SIR-type (compartmental) models - Stochastic Version
Suppose each of N people in a bucket at time t:
Susceptible(t) : not sick, but could get sick
Infected(t) : sick, can make others sick
Removed(t) : recovered or dead; not sick, can’t get sick
- During period \(h\), each \(S\) meets \(kh\) people.
- Assume \(P( S \textrm{ meets } I \textrm{ and becomes } I ) = c\).
- Then \(P( S(t) \rightarrow I(t+h) ) = 1 - (1 - c I(t) / N )^{hk} \approx kchI(t) / N\).
- Therefore, \(I(t+h) | S(t),\ I(t) \sim \textrm{Binom}(S(t),\ kchI(t) / N)\).
- Assume \(P( I(t) \rightarrow R(t+h)) = \gamma h,\ \forall t\).
- Then \(R(t+h) | I_t \sim \textrm{Binom}(I(t),\ \gamma h)\).
SIR-type (compartmental) models - Stochastic Version
In the deterministic limit, \(h\rightarrow 0\)
\[\begin{aligned} \frac{dS}{dt} & = -\frac{\beta}{N} S(t)I(t)\\ \frac{dI}{dt} & = \frac{\beta}{N} I(t)S(t) - \gamma I(t)\\ \frac{dR}{dt} & = \gamma I(t) \end{aligned}\]THE SIR model is often ambiguous between these.
Typically, people mean the deterministic, continuous time version.
Data issues
Ideally we’d observe \(S(t)\), \(I(t)\), \(R(t)\) at all times \(t\)
Easier to observe new infections, \(I(t+h) - I(t)\)
Removals by death are easier to observe than removals by recovery,
so we mostly see \((R(t+h) - R(t)) \times \textrm{(death rate)}\)The interval between measurements, say \(\Delta\), is often \(\gg h\)
Measuring \(I(t)\) and \(R(t)\) (or their rates of change) is hard
- testing/reporting is sporadic and error prone
- Need to model test error (false positives, false negatives) and who gets tested
- Need to model lag between testing and reporting
Parameters (especially, \(\beta\)) change during the epidemic
- Changing behavior, changing policy, environmental factors, vaccines, variants, …
Connecting to Data
Likelihood calculations are straightforward if we can measure \(I_t\), \(R_t\) at all times \(0, h, 2h, \dots, T\)
Or \(I_0\), \(R_0\) and all the increments \(I_{t+h} - I_t\), \(R_{t+h} - R_t\)
Still have to optimize numerically
Likelihood calculations already become difficult if the time between observations \(\Delta \gg h\)
- Generally, \(\Delta \approx\) 1 day
- In principle, this just defines another Markov process, with a longer interval \(\Delta\) between steps, but to get the likelihood of a \(\Delta\) step we have to sum over all possible paths of \(h\) steps adding up to it
Other complications if we don’t observe all the compartments, and/or have a lot of noise in our observations
- We don’t and we do.
Connecting to Data
More tractable to avoid likelihood (Conditional least squares, simulation-based inference)
Intrinsic issue: Initially, everything looks exponential
- Hard to discriminate between distinct models
- If SIR is true, easier to estimate \(\beta - \gamma\) than \((\beta, \gamma)\) or \(\beta/\gamma\)
Can sometimes calibrate or fix the parameters based on other sources
- E.g., \(1/\gamma =\) average time someone is infectious in clinical studies
I have been thinking about how different people interpret data differently. And made this xkcd style graphic to illustrate this. pic.twitter.com/a8LvlmZxT7
— Jens von Bergmann (@vb_jens) March 17, 2021
These models can fit well in-sample
Track observed cases closely (they should)
Can provide nuanced policy advice on some topics
Many questions depend on modulating \(\beta\)
- What happens if we lock down?
- What happens if we mask?
- What happens if we have school online?
- Vaccine passport?
Vaccination modeling is easier, directly removes susceptibles
What about out-of-sample?
2 Operationalizing Compartmental Models
What does this “look like”?
What does this “look like”?
So far, just simulations, how do you fit one?
\[ \begin{aligned} x_{t+1} &= \textrm{OdeSolve}(x_t) + \epsilon_t\\ y_{t+1} &= \textrm{NegBinom}(\textrm{mean} = g(x_t),\ \kappa) \end{aligned} \]
- \(x_t\) is all the compartments
- \(y_t\) are some observations (cases and/or hospitalizations and/or deaths)
- Put priors on all the parameters (they are criminally underidentified)
Turn Bayesian Crank in Stan or similar until you’re done.
{covidseir} model
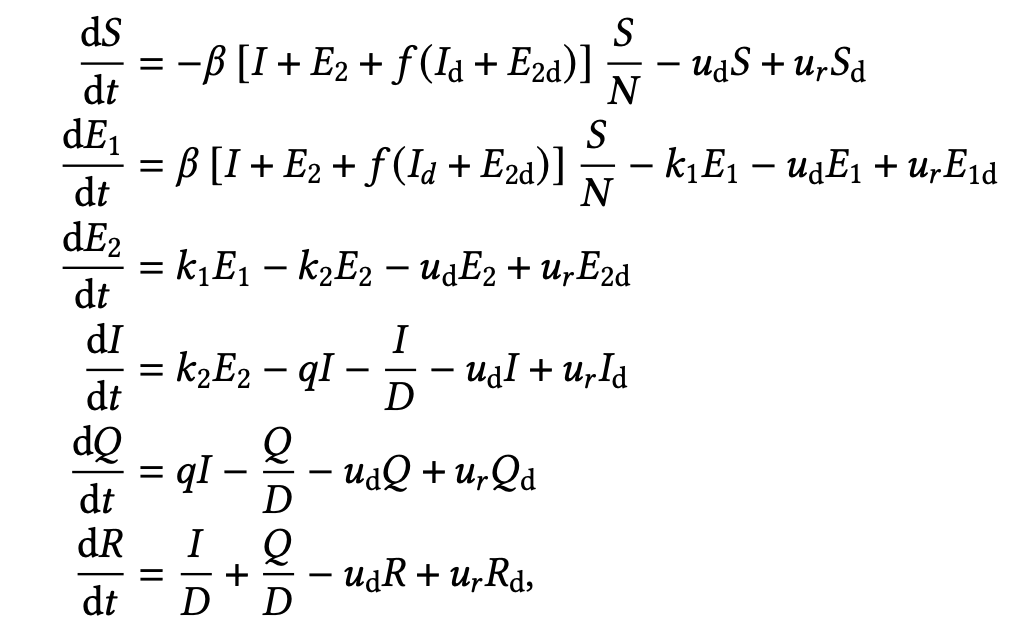
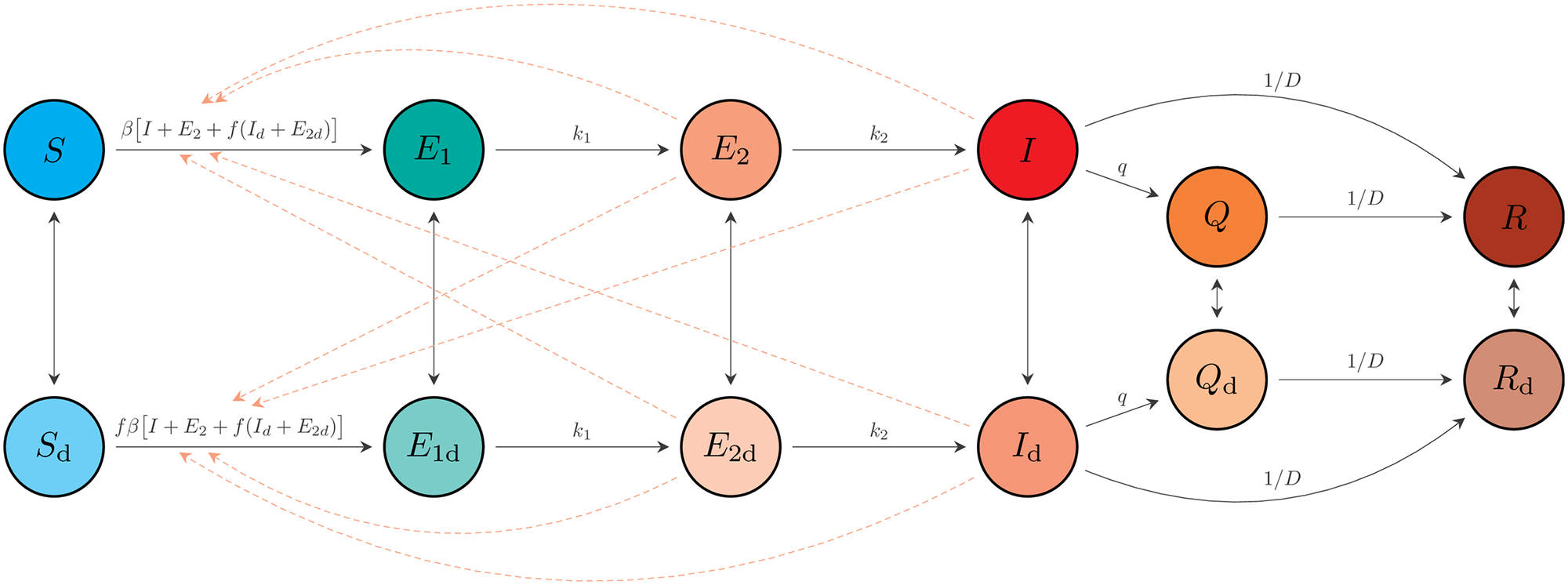
Rpackage: https://seananderson.github.io/covidseir/index.html- Paper link: https://doi.org/10.1371/journal.pcbi.1008274
Fit it to BC data and produce a forecast
samp_frac <- c(rep(0.14, 13), rep(0.21, 38), rep(0.37, nrow(early_bc) - 51))
f_seg <- with(early_bc, case_when(time_value == "2020-03-01" ~ 0, time_value >= "2020-06-01" ~ 3,
time_value >= "2020-05-01" ~ 2, time_value > "2020-03-01" ~ 1))
fit <- covidseir::fit_seir(daily_cases = early_bc$cases,
f_seg = f_seg, # change points in transmission
samp_frac_fixed = samp_frac, # fraction of infections that are tested
iter = 500, # number of posterior samples
fit_type = "optimizing") # for speed onlyUsing this or similar for forecasting
Needed to make lots of assumptions about future epi parameters
- Future transmission rate
- Future case ascertainment rate
- No new variants, or vaccinations, or influx of population
- People don’t lose immunity
- Etc., etc., etc.
More on these as forecasters a bit later.
Better described as scenario models.
3 What is \(R_t\)?
\(R_0\) basic reproduction number
Dates at least to Alfred Lotka (1920s) and others (Feller, Blackwell, etc.)
The expected number of secondary infections due to a primary infection
- \(R_0 < 1\) ⟹ the epidemic will die out
- \(R_0 > 1\) ⟹ the epidemic will grow until everyone is infected
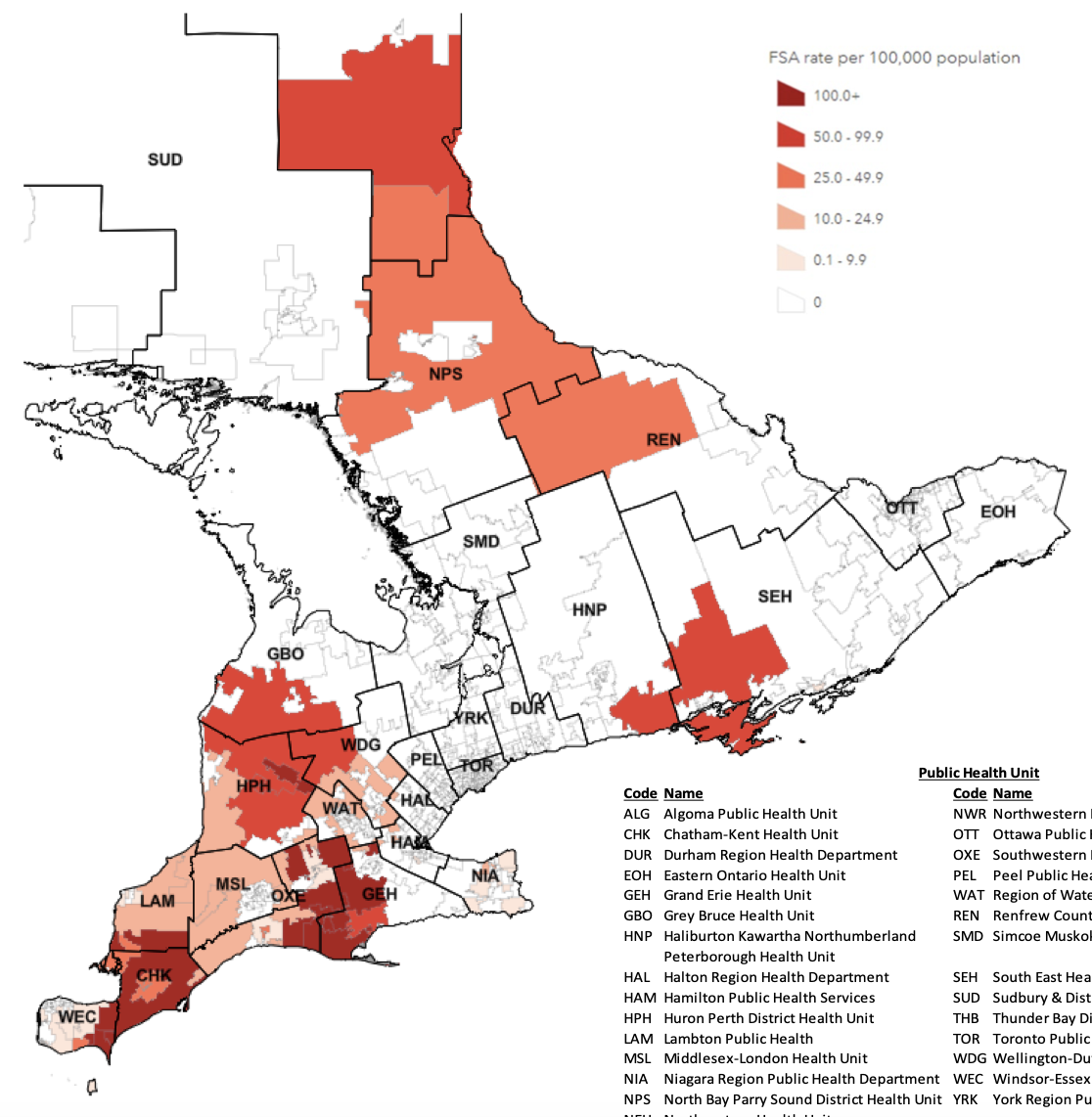
\(R_0\) is entirely retrospective
It’s a property of the pathogen in a fully susceptible (infinite) population
Each outbreak is like a new sample
To estimate something like this from data, the “bonehead” way is to
- Wait until the epidemic is over (no more infections circulating)
- Contact trace the primary infection responsible for each secondary infection
- Take a sample average of the number caused by each primary
- Possibly repeat over many outbreaks
Of course no one actually does that
Lots of work on how to estimate \(R_0\)
Effective reproduction number
Suppose \(s\)% of the population is susceptible
Then, “the” effective reproduction number \(R=sR_0\)
Allows you to reason about things like
The level of vaccine coverage necessary to prevent an outbreak from growing uncontrollably.
So, for measles, if \(R_0\approx 15\), the disease will die out if immunity is
\[ sR_0 \leq 1 \Longrightarrow 1-s \leq 1-1/R_0 \approx 93\% \]
\(R(t)\) — instantaneous reproduction number
The effective reproduction number in the middle of an outbreak
Some of the population is immune, others are infected, others susceptible
The expected number of secondary infections at time \(t\) caused by an earlier primary infection
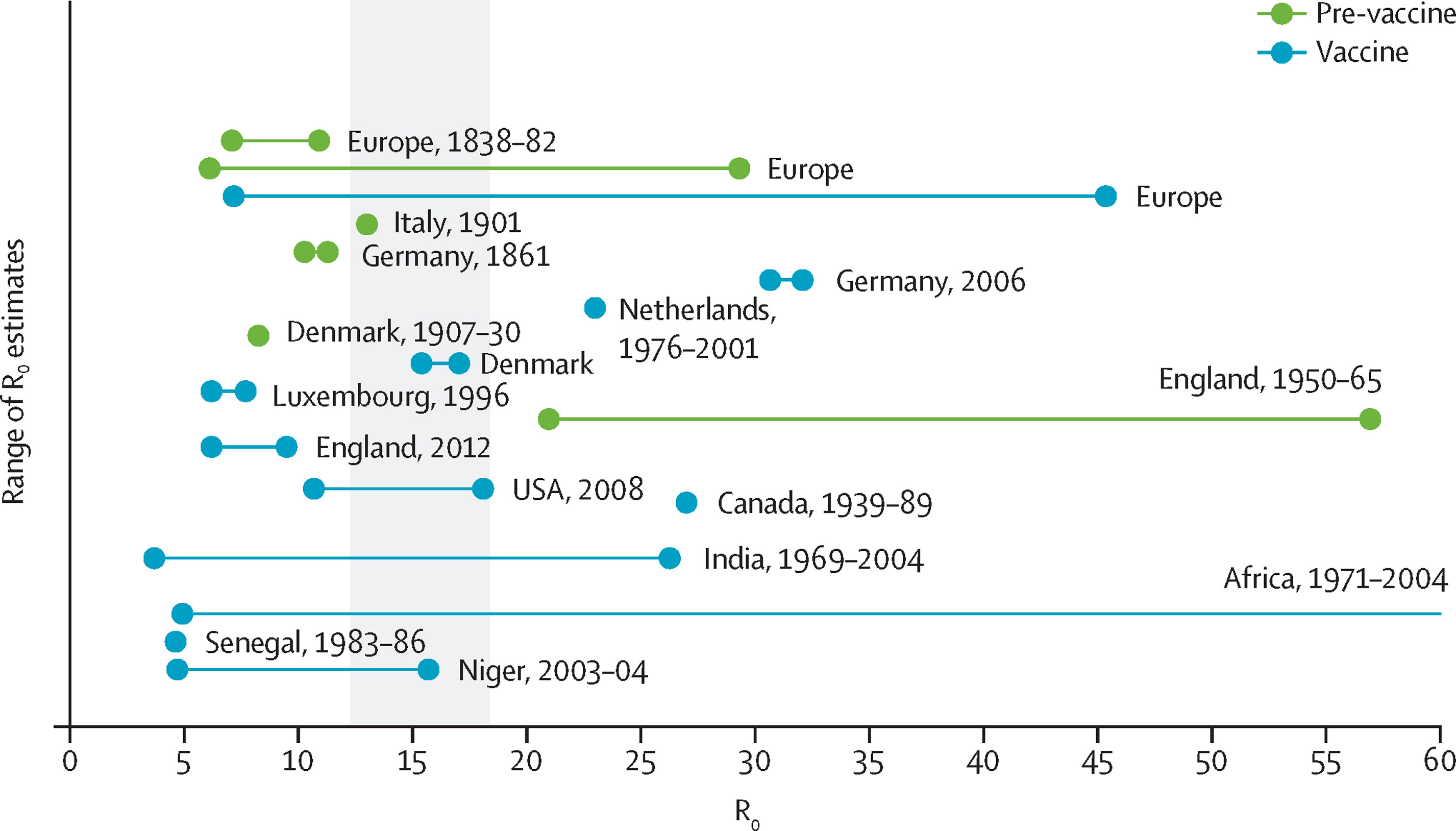
\(f(a) \geq 0,\ \forall a\) — the rate at which an infection of age \(a\) produces new infections
\[ \begin{aligned} R_0 &= \int_{0}^\infty f(a)\mathsf{d}a, \\ g(a) &= \frac{f(a)} {\int_{0}^\infty f(a)\mathsf{d}a} = f(a) / R_0. \end{aligned} \]
Can allow \(g(t, a)\), hold this fixed for now.
The generation interval distribution \(g(a)\)
\(R(t)\) and \(R_t\) — renewal equation
\(R(t)\) is defined implicitly through the renewal equation
\[ x(t) = R(t)\int_0^\infty x(t-a)g(a)\mathsf{d}a, \]
where \(x(t)\) are infections at time \(t\).
In discrete time,
\[ x_{t+1} = R_t\sum_{a=0}^\infty x_{t-a}\widetilde{g}_a = R_t (x * \widetilde{g}). \]
And stochasticly,
\[ \mathbb{E}\big[x_{t+1}\ |\ x_1,\ldots,x_{t}\big] = R_t\sum_{a=0}^\infty x_{t-a}\widetilde{g}_a = R_t (x * \widetilde{g}). \]
Most estimators start here: \[ \mathbb{E}\big[x_{t+1}\ |\ x_1,\ldots,x_{t}\big] = R_t\sum_{a=0}^\infty x_{t-a}\widetilde{g}_a. \]
- Assume \(\widetilde{g}\) is known
- Model \(x_t\ |\ x_1,\ldots,x_{t-1}\) as Poisson or Negative Binomial
- Turn some inferential crank
\(R_t\) for COVID-19 in the US
Source: US CDC Center for Forecasting Analytics
\(R_t\) in compartmental models
There is an equivalence between a compartmental model and the renewal equation.
\[ \begin{aligned} R_0 &= \beta / \gamma\\ x_{t+1} &= \beta S_{t} \sum_{k = 0}^t \big[(1-\gamma)^{k}\big] x_{t-k} = R_0 S_{t} \sum_{k = 0}^t \big[\gamma(1-\gamma)^{k}\big] x_{t-k} = R_{t}\sum_{k = 0}^t g(k)x_{t-k} \end{aligned} \]
4 Estimating \(R_t\)
Data issues
\(x_t\) is Infections, but we don’t ever see those

- Replace infections with cases
- Replace generation interval with serial interval
- Assume we have the serial interval
Serial interval distribution
Standard model for \(R_t\)
\[ \begin{aligned} \eta_t &= \sum_{a=0}^\infty y_{t-a}p_a,\\ \\ y_t\ |\ y_1,\ldots,y_{t-1} &\sim \textrm{Poisson}(R_t\eta_t). \end{aligned} \]
- Using \(y\) instead of \(x\) to be cases or hospitalizations or deaths, incidence
- Using \(p\) for serial interval distribution (discretized)
- The MLE for \(R_t\) is just \(y_t / \eta_t\).
- This has really high variance, but unbiased.
- So everybody smooths it.
The state of the art
{EpiEstim}(Cori, et al., 2013)
- Gamma prior on \(R_t\), but use a trailing window
- Super fast computationally
- Smoothness is ad hoc
{EpiFilter}(Parag, 2020)
- State space model
- One step smoothness: \(R_{s+1} \sim \textrm{Gaussian}(R_s,\ \alpha R_s)\)
- Uses a discretized particle filter-type algorithm
{EpiLPS}(Gressani, et al., 2022)
- Negative Binomial likelihood
- Smoothness via \(\log(R_t\eta_t) = \mathbf{B}_{t,:}\beta\)
- \(\mathbf{B}\) is cubic B-spline basis, weighted Ridge penalty on \(\beta\)
- More priors, use Metropolis Adjusted Langevin Algorithm
{EpiNow2}(CDC + CFA, Abbott, et al., 2023ish)
- Negative Binomial likelihood
- Smoothness via a GP prior
- Accommodates the sequence of delays from infection \(\longrightarrow\) ??
- Adjusts for real-time issues like partial reporting
- Big Bayesian MCMC in Stan. Very slow.
Our model
Let \(\theta_t := \log(R_t)\).
Use Poisson likelihood.
\[ \begin{aligned} \widehat{R} &= \exp(\widehat{\theta}) &\widehat{\theta} &= \mathop{\mathrm{argmin}}_\theta\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(k+1)}\theta\Vert_1 \end{aligned} \]
- Convex, has a global optimum
- \(\lambda\) controls smoothness relative to data fidelity
- \(\ell_1\) penalty produces adaptive piecewise polynomials of order \(k+1\)
- Near minimax optimal for functions with bounded total variation
Local adaptivity — \(\ell_1\) vs. \(\ell_2\)
Polynomial order, \(k=0\)
\[
\begin{aligned}
D^{(1)} &= \begin{bmatrix}
1 & -1 & & & & \\
& 1 & -1 & & & \\
& & & \ddots && \\
& & & & 1 & -1
\end{bmatrix} \\ \\
&\in \mathbb{R}^{(n-1)\times n}
\end{aligned}
\]
Polynomial order, \(k=1\)
\[
\begin{aligned}
D^{(2)} &= \begin{bmatrix}
1 & -2 & 1 & & & \\
& 1 & -2 & 1 & & \\
& & & \ddots && \\
& & & 1 & -2 & 1
\end{bmatrix} \\ \\
&= D^{(1)}D^{(1)}\\ \\
&\in \mathbb{R}^{(n-k-1)\times n}
\end{aligned}
\]
Polynomial order, \(k=2\)
\[
\begin{aligned}
D^{(3)} &= \begin{bmatrix}
-1 & 3 & -3 & 1 & & \\
& -1 & 3 & -3 &1 & \\
& & & \ddots && \\
& & -1 & 3 & -3 & 1
\end{bmatrix} \\ \\
&= D^{(1)}D^{(2)}\\ \\
&\in \mathbb{R}^{(n-k-1)\times n}
\end{aligned}
\]
Estimation algorithm
\[ \mathop{\mathrm{minimize}}_\theta\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(k+1)}\theta\Vert_1 \]
Estimation algorithm
\[ \mathop{\mathrm{minimize}}_{\theta,\ {\color{BurntOrange} \alpha}}\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(1)}{\color{BurntOrange} \alpha}\Vert_1\quad {\color{BurntOrange} \textrm{subject to}\quad \alpha = D^{(k)}\theta} \]
Estimation algorithm
\[ \mathop{\mathrm{minimize}}_{\theta,\ \alpha}\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(1)} \alpha\Vert_1\quad \textrm{subject to}\quad \alpha = D^{(k)}\theta \]
Alternating direction method of multipliers (ADMM)
\[ \begin{aligned} \theta &\longleftarrow \mathop{\mathrm{argmin}}_\theta\ \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \frac{\rho}{2}\Vert D^{(k)}\theta - \alpha + u \Vert_2^2 \\ \alpha &\longleftarrow \mathop{\mathrm{argmin}}_\alpha\ \lambda\Vert D^{(1)} \alpha \Vert_1 + \frac{\rho}{2}\Vert D^{(k)}\theta - \alpha + u \Vert_2^2 \\ u &\longleftarrow u + D^{(k)}\theta - \alpha \end{aligned} \]
Estimation algorithm
\[ \mathop{\mathrm{minimize}}_{\theta,\ \alpha}\; \eta^{\mathsf{T}}\exp(\theta) - \mathbf{y}^{\mathsf{T}}\theta + \lambda\Vert D^{(1)} \alpha\Vert_1\quad \textrm{subject to}\quad \alpha = D^{(k)}\theta \]
Alternating direction method of multipliers (ADMM)
\[ \begin{aligned} \theta &\longleftarrow {\color{Cerulean}\textrm{Proximal Newton / Fisher Scoring}} \\ \alpha &\longleftarrow {\color{BurntOrange}\textrm{Fused Lasso Signal Approximator}} \\ u &\longleftarrow u + D^{(k)}\theta - \alpha \end{aligned} \]
Solve sequentially for \(\Vert (D^{\dagger})^{\mathsf{T}}(\eta - y)\Vert_\infty = \lambda_1 > \cdots > \lambda_M=\epsilon \lambda_1\).
5 Results and features of {rtestim}
Canadian Covid-19 cases
\(R_t\) for Canadian Covid-19 cases
Reconvolved Canadian Covid-19 cases
Example simulations for different methods
{rtestim} software
Guts are in C++ for speed
Lots of the usual S3 methods
Approximate “confidence” bands
\(\widehat{R}\) is a member of a function space
Arbitrary spacing of observations
Built-in cross validation
Time-varying delay distributions
{rtestim} software
Guts are in C++ for speed
Lots of the usual S3 methods
Approximate “confidence” bands
\(\widehat{R}\) is a member of a function space
Arbitrary spacing of observations
Built-in cross validation
Time-varying delay distributions
Approximation + Delta method gives
\[ \textrm{Var}(\widehat{R}) = \left(\textrm{diag}(\widehat{y}) + \lambda D^{\mathsf{T}}D\right)^{\dagger} \left(\frac{1}{\eta^2}\right) \]
{rtestim} software
Guts are in C++ for speed
Lots of the usual S3 methods
Approximate “confidence” bands
\(\widehat{R}\) is a member of a function space
Arbitrary spacing of observations
Built-in cross validation
Time-varying delay distributions
The solution is an element of the space of discrete splines of order \(k\) (Tibshirani, 2020)
- Lets us interpolate (and extrapolate) to off-observation points
- Lets us handle uneven spacing
{rtestim} software
Guts are in C++ for speed
Lots of the usual S3 methods
Approximate “confidence” bands
\(\widehat{R}\) is a member of a function space
Arbitrary spacing of observations
Built-in cross validation
Time-varying delay distributions
{rtestim} software
Wrapup and practice
- Basic compartmental modelling
- Difficulties in estimating compartmental models
- Standard epidemic parameters, \(R_0\)
- Discussion of \(R_t\) (model based vs nonparametric estimation)
- Some custom \(R_t\) software

Epi models — dajmcdon/canssip-epidata-2025